9 логических задач, которые по зубам только настоящим интеллектуалам

1. День рождения Шерил
Предположим, некие Бернард и Альберт недавно познакомились с девушкой Шерил. Они хотят узнать, когда у неё день рождения — чтобы приготовить подарки. Но Шерил та ещё штучка. Вместо ответа она вручает парням список из 10 возможных дат:
| 15 мая | 16 мая | 19 мая |
| 17 июня | 18 июня | |
| 14 июля | 16 июля | |
| 14 августа | 15 августа | 17 августа |
Предсказуемо обнаружив, что юноши не могут вычислить правильную дату, Шерил шёпотом, на ухо, называет Альберту только месяц её рождения. А Бернарду — также тихо — лишь число.
— Хм, — говорит Альберт. — Я не знаю, когда у Шерил день рождения. Но я точно знаю, что Бернард этого тоже не знает.
— Ха, — отвечает Бернард. — Сначала я тоже не знал, когда у Шерил день рождения, но теперь знаю это!
— Ага, — соглашается Альберт. — Теперь я тоже знаю.
И они хором называют верную дату. Когда же у Шерил день рождения?
Если у вас не получается с ходу найти ответ, не расстраивайтесь. Впервые этот вопрос прозвучал на подростковой математической олимпиаде в , который славится высочайшими образовательными стандартами. После того как один из местных телеведущих опубликовал скрин этой задачки в Facebook*, она стала : решить её пытались десятки тысяч пользователей Facebook*, Twitter, Reddit. Но справились не все.
Мы уверены, что у вас получится. Не открывайте отгадку, пока хотя бы не попробуете.
2. Сколько лет дочкам
На улице однажды встретились два бывших одноклассника, и между ними состоялся такой диалог.
— Привет!
— Привет!
— Как дела?
— Хорошо. Растут две дочери, дошкольницы ещё.
— А сколько им лет?
— Ну‑у‑у… Произведение их возрастов равно числу голубей у нас под ногами.
— Этой информации мне недостаточно!
— Старшая похожа на мать.
— Вот теперь я знаю ответ на свой вопрос!
Так сколько же лет дочкам одного из собеседников?
3. Где моя машина?!
Говорят, эту задачу задают ученикам младших классов гонконгских школ. Дети решают её буквально за считаные секунды.
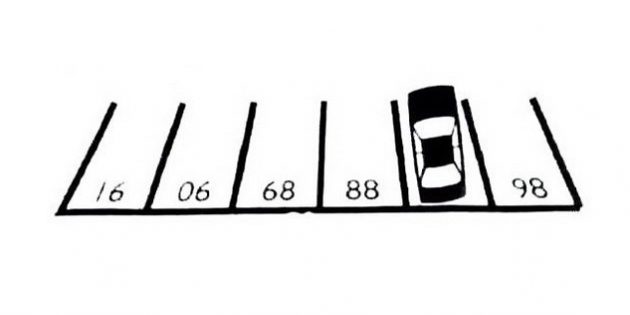
Назовите номер парковочного места, которое занимает автомобиль.
4. Любовь в Клептопии
Ян и Мария полюбили друг друга, общаясь только через интернет. Ян хочет отправить Марии обручальное кольцо по почте — чтобы сделать предложение. Но вот беда: возлюбленные живут в стране Клептопии, где любая посылка, передаваемая по почте, обязательно будет украдена — если только её не заключить в ящик с замком.
У Яна и Марии много замков, но отправить друг другу ключи они не могут — ведь ключи тоже будут украдены. Как Яну отправить кольцо, чтобы оно наверняка попало Марии в руки?
5. В поисках подделки
Курьер принёс вам 10 сумок, в каждой из которых очень много монет. И всё бы хорошо, но вы подозреваете, что деньги в одной из сумок фальшивые. Всё, что вам известно наверняка, — это то, что настоящие монеты весят 1 г каждая, а поддельные — 1,1 г. Других отличий между денежками нет.
На счастье, у вас есть точные цифровые весы, показывающие вес вплоть до десятой грамма. Но курьер очень торопится.
Словом, времени нет, вам даётся лишь одна попытка воспользоваться весами. Как за одно взвешивание точно вычислить, в какой именно сумке находятся поддельные монеты и есть ли такая сумка вообще?
6. Равенство решек
В тёмной‑тёмной (вот вообще ни зги не видать, и свет включить нельзя) комнате стоит стол, на котором лежат 50 монет. Вы их не видите, но можете пощупать, перевернуть. И главное, точно знаете: 40 монет изначально лежат орлом вверх, а 10 — решкой.
Ваша задача — разделить деньги на две группы (не обязательно равные), в каждой из которых будет одинаковое количество монеток решкой вверх.
7. Как не выйти замуж
Однажды хозяин мелкой лавки в Италии задолжал ростовщику крупную сумму. Возможности отдать долг у него не было. Зато была красавица‑дочь, которая давно нравилась кредитору.
— Давай сделаем так, — предложил лавочнику ростовщик. — Ты выдаёшь дочь за меня, а я по‑родственному забываю о долге. Ну что, по рукам?
Но девушка не хотела выходить замуж за старого и некрасивого мужчину. Поэтому лавочник ответил отказом. Однако потенциальный зять уловил в его голосе колебание и сделал новое предложение.
— Я не хочу никого принуждать, — мягко сказал ростовщик. — Пусть всё за нас решит случай. Смотри: я положу в мешочек два камня — чёрный и белый. И пусть дочка не глядя вытащит один из них. Если это будет чёрный, мы с ней поженимся и я прощу тебе долг. Если белый — я прощу долг просто так, не требуя руки твоей дочери.
Сделка выглядела справедливой, и на этот раз отец согласился. Ростовщик наклонился к дорожке, усыпанной галькой, быстро поднял камни и положил их в мешочек. Но дочь заметила ужасное: оба камушка были чёрными! Какой бы она ни вытащила, ей пришлось бы выходить замуж. Конечно, можно было уличить ростовщика в обмане, вынув сразу оба камня. Но тот мог бы прийти в ярость и отменить сделку, затребовав долг в полном объёме.
Подумав пару секунд, девушка уверенно протянула руку к мешочку. И сделала кое‑что, что избавило её отца от долга, а её саму — от необходимости замужества. Справедливость её поступка признал даже ростовщик. Что именно она сделала?
8. У вас код запутался…
Вы закрыли чемодан на цифровой замок с трёхзначным кодом и случайно забыли цифры. Но память предлагает вам следующие подсказки:
- 682 — в этом коде одна из цифр верна и стоит на своём месте;
- 614 — одна из цифр правильная, но стоит не на своём месте;
- 206 — верны две цифры, но обе стоят не на своих местах;
- 738 — вообще чепуха, ни одного попадания;
- 870 — одна цифра верная, но не на своём месте.
Этой информации хватает, чтобы подобрать правильный код. Какой он?
9. Как поделить торт
И напоследок немного сладкого. У вас есть праздничный торт, который надо разделить по числу гостей — на 8 кусков. Проблема лишь в том, что это необходимо сделать, совершив всего три разреза. Справитесь?
*Деятельность Meta Platforms Inc. и принадлежащих ей социальных сетей Facebook и Instagram запрещена на территории РФ.
















Лучшие предложения
Находки AliExpress: самые интересные и полезные товары недели
15 товаров с AliExpress для тех, кому надоел интерьер дома
Надо брать: демисезонные кроссовки от Baasploa со скидкой 69%
10 вещей с маркетплейсов, которые порадовали нас на этой неделе
Флагманский робот-пылесос от Roborock отдают со скидкой 56% на AliExpress
10 популярных товаров с приличными скидками на AliExpress
Оформляем дебетовку с кешбэком до 15% за пополнение PS Store, Steam и Xbox
Дешевле 3 000 рублей стоит хороший мойщик окон прямо сейчас на AliExpress
Культурный челлендж: 6 способов получить новые впечатления в этом году
Как сегодня в России создают новые лекарства и учатся «заживлять» трещины в металле
Уколы для похудения «Седжаро»: что нужно знать о препарате
Планирование беременности: какие обследования нужно пройти